Attention (machine learning)
In today's world, Attention (machine learning) is a topic that has captured the attention of a large number of people. Whether due to its relevance in society, its impact on popular culture or its importance in history, Attention (machine learning) has become a topic of interest for many. In this article, we will explore different aspects related to Attention (machine learning), from its origin and evolution to its influence in various areas. Through detailed and exhaustive analysis, we will seek to shed light on this topic and provide a clear and comprehensive perspective for our readers.
| Part of a series on |
| Machine learning and data mining |
|---|

Attention is a machine learning method that determines the relative importance of each component in a sequence relative to the other components in that sequence. In natural language processing, importance is represented by "soft" weights assigned to each word in a sentence. More generally, attention encodes vectors called token embeddings across a fixed-width sequence that can range from tens to millions of tokens in size.
Unlike "hard" weights, which are computed during the backwards training pass, "soft" weights exist only in the forward pass and therefore change with every step of the input. Earlier designs implemented the attention mechanism in a serial recurrent neural network (RNN) language translation system, but a more recent design, namely the transformer, removed the slower sequential RNN and relied more heavily on the faster parallel attention scheme.
Inspired by ideas about attention in humans, the attention mechanism was developed to address the weaknesses of leveraging information from the hidden layers of recurrent neural networks. Recurrent neural networks favor more recent information contained in words at the end of a sentence, while information earlier in the sentence tends to be attenuated. Attention allows a token equal access to any part of a sentence directly, rather than only through the previous state.
History
| 1950's 1960's | Psychology biology of attention. cocktail party effect [1] - focusing on content by filtering out background noise. filter model of attention,[2] partial report paradigm, and saccade control.[3]
1965 - Group Method of Data Handling[4][5] (Kolmogorov-Gabor polynomials implement multiplicative units or "gates"[6]) |
| 1980's | sigma pi units,[7] higher order neural networks[8]
Neocognitron and its variants.[9][10] |
| 1990's | fast weight controller. [11][12][13][14] Neuron weights generate fast "dynamic links" similar to keys & values.[15] |
| 2014 |
RNN + Attention.[16] Attention network was grafted onto RNN encoder decoder to improve language translation of long sentences. See Overview section. |
| 2015 | Attention applied to images [17] [18] [19] |
| 2017 | Transformers [20] = Attention + position encoding + MLP + skip connections. This design improved accuracy and removed the sequential disadvantages of the RNN. |
Academic reviews of the history of the attention mechanism are provided in Niu et al.[21] and Soydaner.[22]
Overview
The modern era of machine attention was revitalized by grafting an attention mechanism (Fig 1. orange) to an Encoder-Decoder.
 Fig 1. Encoder-decoder with attention.[23] Numerical subscripts (100, 300, 500, 9k, 10k) indicate vector sizes while lettered subscripts i and i − 1 indicate time steps. Pinkish regions in H matrix and w vector are zero values. See Legend for details.
|
Figure 2 shows the internal step-by-step operation of the attention block (A) in Fig 1.
- This example focuses on the attention of a single word "that". In practice, the attention of each word is calculated in parallel to speed up calculations. Simply changing the lowercase "x" vector to the uppercase "X" matrix will yield the formula for this.
- Softmax scaling qWkT / √100 prevents a high variance in qWkT that would allow a single word to excessively dominate the softmax resulting in attention to only one word, as a discrete hard max would do.
- Notation: the commonly written row-wise softmax formula above assumes that vectors are rows, which runs contrary to the standard math notation of column vectors. More correctly, we should take the transpose of the context vector and use the column-wise softmax, resulting in the more correct form
This attention scheme has been compared to the Query-Key analogy of relational databases. That comparison suggests an asymmetric role for the Query and Key vectors, where one item of interest (the Query vector "that") is matched against all possible items (the Key vectors of each word in the sentence). However, both Self and Cross Attentions' parallel calculations matches all tokens of the K matrix with all tokens of the Q matrix; therefore the roles of these vectors are symmetric. Possibly because the simplistic database analogy is flawed, much effort has gone into understanding attention mechanisms further by studying their roles in focused settings, such as in-context learning,[25] masked language tasks,[26] stripped down transformers,[27] bigram statistics,[28] N-gram statistics,[29] pairwise convolutions,[30] and arithmetic factoring.[31]
Interpreting attention weights
In translating between languages, alignment is the process of matching words from the source sentence to words of the translated sentence. Networks that perform verbatim translation without regard to word order would show the highest scores along the (dominant) diagonal of the matrix. The off-diagonal dominance shows that the attention mechanism is more nuanced.
Consider an example of translating I love you to French. On the first pass through the decoder, 94% of the attention weight is on the first English word I, so the network offers the word je. On the second pass of the decoder, 88% of the attention weight is on the third English word you, so it offers t'. On the last pass, 95% of the attention weight is on the second English word love, so it offers aime.
In the I love you example, the second word love is aligned with the third word aime. Stacking soft row vectors together for je, t', and aime yields an alignment matrix:
| I | love | you | |
|---|---|---|---|
| je | 0.94 | 0.02 | 0.04 |
| t' | 0.11 | 0.01 | 0.88 |
| aime | 0.03 | 0.95 | 0.02 |
Sometimes, alignment can be multiple-to-multiple. For example, the English phrase look it up corresponds to cherchez-le. Thus, "soft" attention weights work better than "hard" attention weights (setting one attention weight to 1, and the others to 0), as we would like the model to make a context vector consisting of a weighted sum of the hidden vectors, rather than "the best one", as there may not be a best hidden vector.
Variants

Many variants of attention implement soft weights, such as
- fast weight programmers, or fast weight controllers (1992).[11] A "slow" neural network outputs the "fast" weights of another neural network through outer products. The slow network learns by gradient descent. It was later renamed as "linearized self-attention".[15]
- Bahdanau-style attention,[16] also referred to as additive attention,
- Luong-style attention,[32] which is known as multiplicative attention,
- highly parallelizable self-attention introduced in 2016 as decomposable attention[33] and successfully used in transformers a year later,
- positional attention and factorized positional attention.[34]
For convolutional neural networks, attention mechanisms can be distinguished by the dimension on which they operate, namely: spatial attention,[35] channel attention,[36] or combinations.[37][38]
These variants recombine the encoder-side inputs to redistribute those effects to each target output. Often, a correlation-style matrix of dot products provides the re-weighting coefficients. In the figures below, W is the matrix of context attention weights, similar to the formula in Core Calculations section above.
| 1. encoder-decoder dot product | 2. encoder-decoder QKV | 3. encoder-only dot product | 4. encoder-only QKV | 5. Pytorch tutorial |
|---|---|---|---|---|
 |
 |
 |
 |
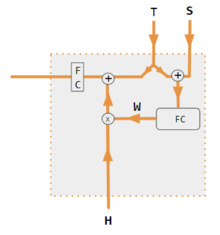 |
| Label | Description |
|---|---|
| Variables X, H, S, T | Upper case variables represent the entire sentence, and not just the current word. For example, H is a matrix of the encoder hidden state—one word per column. |
| S, T | S, decoder hidden state; T, target word embedding. In the Pytorch Tutorial variant training phase, T alternates between 2 sources depending on the level of teacher forcing used. T could be the embedding of the network's output word; i.e. embedding(argmax(FC output)). Alternatively with teacher forcing, T could be the embedding of the known correct word which can occur with a constant forcing probability, say 1/2. |
| X, H | H, encoder hidden state; X, input word embeddings. |
| W | Attention coefficients |
| Qw, Kw, Vw, FC | Weight matrices for query, key, value respectively. FC is a fully-connected weight matrix. |
| ⊕, ⊗ | ⊕, vector concatenation; ⊗, matrix multiplication. |
| corr | Column-wise softmax(matrix of all combinations of dot products). The dot products are xi * xj in variant #3, hi* sj in variant 1, and column i ( Kw * H ) * column j ( Qw * S ) in variant 2, and column i ( Kw * X ) * column j ( Qw * X ) in variant 4. Variant 5 uses a fully-connected layer to determine the coefficients. If the variant is QKV, then the dot products are normalized by the √d where d is the height of the QKV matrices. |
Optimizations
Flash attention
The size of the attention matrix is proportional to the square of the number of input tokens. Therefore, when the input is long, calculating the attention matrix requires a lot of GPU memory. Flash attention is an implementation that reduces the memory needs and increases efficiency without sacrificing accuracy. It achieves this by partitioning the attention computation into smaller blocks that fit into the GPU's faster on-chip memory, reducing the need to store large intermediate matrices and thus lowering memory usage while increasing computational efficiency.[43]
Mathematical representation
Standard Scaled Dot-Product Attention
For matrices: and , the scaled dot-product, or QKV attention is defined as: where denotes transpose and the softmax function is applied independently to every row of its argument. The matrix contains queries, while matrices jointly contain an unordered set of key-value pairs. Value vectors in matrix are weighted using the weights resulting from the softmax operation, so that the rows of the -by- output matrix are confined to the convex hull of the points in given by the rows of .
To understand the permutation invariance and permutation equivariance properties of QKV attention,[44] let and be permutation matrices; and an arbitrary matrix. The softmax function is permutation equivariant in the sense that:
By noting that the transpose of a permutation matrix is also its inverse, it follows that:
which shows that QKV attention is equivariant with respect to re-ordering the queries (rows of ); and invariant to re-ordering of the key-value pairs in . These properties are inherited when applying linear transforms to the inputs and outputs of QKV attention blocks. For example, a simple self-attention function defined as:
is permutation equivariant with respect to re-ordering the rows of the input matrix in a non-trivial way, because every row of the output is a function of all the rows of the input. Similar properties hold for multi-head attention, which is defined below.
Masked Attention
When QKV attention is used as a building block for an autoregressive decoder, and when at training time all input and output matrices have rows, a masked attention variant is used: where the mask, is a strictly upper triangular matrix, with zeros on and below the diagonal and in every element above the diagonal. The softmax output, also in is then lower triangular, with zeros in all elements above the diagonal. The masking ensures that for all , row of the attention output is independent of row of any of the three input matrices. The permutation invariance and equivariance properties of standard QKV attention do not hold for the masked variant.
Multi-Head Attention

Multi-head attention where each head is computed with QKV attention as: and , and are parameter matrices.
The permutation properties of (standard, unmasked) QKV attention apply here also. For permutation matrices, :
from which we also see that multi-head self-attention:
is equivariant with respect to re-ordering of the rows of input matrix .
Bahdanau (Additive) Attention
where and are learnable weight matrices.[16]
Luong Attention (General)
where is a learnable weight matrix.[32]
Self Attention
Self-attention is essentially the same as cross-attention, except that query, key, and value vectors all come from the same model. Both encoder and decoder can use self-attention, but with subtle differences.
For encoder self-attention, we can start with a simple encoder without self-attention, such as an "embedding layer", which simply converts each input word into a vector by a fixed lookup table. This gives a sequence of hidden vectors . These can then be applied to a dot-product attention mechanism, to obtainor more succinctly, . This can be applied repeatedly, to obtain a multilayered encoder. This is the "encoder self-attention", sometimes called the "all-to-all attention", as the vector at every position can attend to every other.
Masking

For decoder self-attention, all-to-all attention is inappropriate, because during the autoregressive decoding process, the decoder cannot attend to future outputs that has yet to be decoded. This can be solved by forcing the attention weights for all , called "causal masking". This attention mechanism is the "causally masked self-attention".
See also
- Recurrent neural network
- seq2seq
- Transformer (deep learning architecture)
- Attention
- Dynamic neural network
References
- ^ Cherry EC (1953). "Some Experiments on the Recognition of Speech, with One and with Two Ears" (PDF). The Journal of the Acoustical Society of America. 25 (5): 975–79. Bibcode:1953ASAJ...25..975C. doi:10.1121/1.1907229. hdl:11858/00-001M-0000-002A-F750-3. ISSN 0001-4966.
- ^ Broadbent, D (1958). Perception and Communication. London: Pergamon Press.
- ^ Kowler, Eileen; Anderson, Eric; Dosher, Barbara; Blaser, Erik (1995-07-01). "The role of attention in the programming of saccades". Vision Research. 35 (13): 1897–1916. doi:10.1016/0042-6989(94)00279-U. ISSN 0042-6989. PMID 7660596.
- ^ Ivakhnenko, A. G. (1973). Cybernetic Predicting Devices. CCM Information Corporation.
- ^ Ivakhnenko, A. G.; Grigorʹevich Lapa, Valentin (1967). Cybernetics and forecasting techniques. American Elsevier Pub. Co.
- ^ Schmidhuber, Jürgen (2022). "Annotated History of Modern AI and Deep Learning". arXiv:2212.11279 .
- ^ Rumelhart, David E.; Hinton, G. E.; Mcclelland, James L. (1987-07-29). "A General Framework for Parallel Distributed Processing" (PDF). In Rumelhart, David E.; Hinton, G. E.; PDP Research Group (eds.). Parallel Distributed Processing, Volume 1: Explorations in the Microstructure of Cognition: Foundations. Cambridge, Massachusetts: MIT Press. ISBN 978-0-262-68053-0.
- ^ Giles, C. Lee; Maxwell, Tom (1987-12-01). "Learning, invariance, and generalization in high-order neural networks". Applied Optics. 26 (23): 4972–4978. doi:10.1364/AO.26.004972. ISSN 0003-6935. PMID 20523475.
- ^ Fukushima, Kunihiko (1987-12-01). "Neural network model for selective attention in visual pattern recognition and associative recall". Applied Optics. 26 (23): 4985–4992. Bibcode:1987ApOpt..26.4985F. doi:10.1364/AO.26.004985. ISSN 0003-6935. PMID 20523477.
- ^ Ba, Jimmy; Mnih, Volodymyr; Kavukcuoglu, Koray (2015-04-23). "Multiple Object Recognition with Visual Attention". arXiv:1412.7755 .
- ^ a b Schmidhuber, Jürgen (1992). "Learning to control fast-weight memories: an alternative to recurrent nets". Neural Computation. 4 (1): 131–139. doi:10.1162/neco.1992.4.1.131. S2CID 16683347.
- ^ Christoph von der Malsburg: The correlation theory of brain function. Internal Report 81-2, MPI Biophysical Chemistry, 1981. http://cogprints.org/1380/1/vdM_correlation.pdf See Reprint in Models of Neural Networks II, chapter 2, pages 95-119. Springer, Berlin, 1994.
- ^ Jerome A. Feldman, "Dynamic connections in neural networks," Biological Cybernetics, vol. 46, no. 1, pp. 27-39, Dec. 1982.
- ^ Hinton, Geoffrey E.; Plaut, David C. (1987). "Using Fast Weights to Deblur Old Memories". Proceedings of the Annual Meeting of the Cognitive Science Society. 9.
- ^ a b Schlag, Imanol; Irie, Kazuki; Schmidhuber, Jürgen (2021). "Linear Transformers Are Secretly Fast Weight Programmers". ICML 2021. Springer. pp. 9355–9366.
- ^ a b c Bahdanau, Dzmitry; Cho, Kyunghyun; Bengio, Yoshua (2014). "Neural Machine Translation by Jointly Learning to Align and Translate". arXiv:1409.0473 .
- ^ Vinyals, Oriol; Toshev, Alexander; Bengio, Samy; Erhan, Dumitru (2015). "Show and Tell: A Neural Image Caption Generator". pp. 3156–3164.
- ^ Xu, Kelvin; Ba, Jimmy; Kiros, Ryan; Cho, Kyunghyun; Courville, Aaron; Salakhudinov, Ruslan; Zemel, Rich; Bengio, Yoshua (2015-06-01). "Show, Attend and Tell: Neural Image Caption Generation with Visual Attention". Proceedings of the 32nd International Conference on Machine Learning. PMLR: 2048–2057.
- ^ Bahdanau, Dzmitry; Cho, Kyunghyun; Bengio, Yoshua (19 May 2016). "Neural Machine Translation by Jointly Learning to Align and Translate". arXiv:1409.0473 . (orig-date 1 Sep 2014)
- ^ Vaswani, Ashish; Shazeer, Noam; Parmar, Niki; Uszkoreit, Jakob; Jones, Llion; Gomez, Aidan N; Kaiser, Łukasz; Polosukhin, Illia (2017). "Attention is All you Need" (PDF). Advances in Neural Information Processing Systems. 30. Curran Associates, Inc.
- ^ Niu, Zhaoyang; Zhong, Guoqiang; Yu, Hui (2021-09-10). "A review on the attention mechanism of deep learning". Neurocomputing. 452: 48–62. doi:10.1016/j.neucom.2021.03.091. ISSN 0925-2312.
- ^ Soydaner, Derya (August 2022). "Attention mechanism in neural networks: where it comes and where it goes". Neural Computing and Applications. 34 (16): 13371–13385. arXiv:2204.13154. doi:10.1007/s00521-022-07366-3. ISSN 0941-0643.
- ^ Britz, Denny; Goldie, Anna; Luong, Minh-Thanh; Le, Quoc (2017-03-21). "Massive Exploration of Neural Machine Translation Architectures". arXiv:1703.03906 .
- ^ "Pytorch.org seq2seq tutorial". Retrieved December 2, 2021.
- ^ Zhang, Ruiqi (2024). "Trained Transformers Learn Linear Models In-Context" (PDF). Journal of Machine Learning Research 1-55. 25. arXiv:2306.09927.
- ^ Rende, Riccardo (2024). "Mapping of attention mechanisms to a generalized Potts model". Physical Review Research. 6 (2): 023057. arXiv:2304.07235. Bibcode:2024PhRvR...6b3057R. doi:10.1103/PhysRevResearch.6.023057.
- ^ He, Bobby (2023). "Simplifying Transformers Blocks". arXiv:2311.01906 .
- ^ Nguyen, Timothy (2024). "Understanding Transformers via N-gram Statistics". arXiv:2407.12034 .
- ^ "Transformer Circuits". transformer-circuits.pub.
- ^ Transformer Neural Network Derived From Scratch. 2023. Event occurs at 05:30. Retrieved 2024-04-07.
- ^ Charton, François (2023). "Learning the Greatest Common Divisor: Explaining Transformer Predictions". arXiv:2308.15594 .
- ^ a b c Luong, Minh-Thang (2015-09-20). "Effective Approaches to Attention-Based Neural Machine Translation". arXiv:1508.04025v5 .
- ^ Cheng, Jianpeng; Dong, Li; Lapata, Mirella (2016-09-20). "Long Short-Term Memory-Networks for Machine Reading". arXiv:1601.06733 .
- ^ "Learning Positional Attention for Sequential Recommendation". catalyzex.com.
- ^ Zhu, Xizhou; Cheng, Dazhi; Zhang, Zheng; Lin, Stephen; Dai, Jifeng (2019). "An Empirical Study of Spatial Attention Mechanisms in Deep Networks". 2019 IEEE/CVF International Conference on Computer Vision (ICCV). pp. 6687–6696. arXiv:1904.05873. doi:10.1109/ICCV.2019.00679. ISBN 978-1-7281-4803-8. S2CID 118673006.
- ^ Hu, Jie; Shen, Li; Sun, Gang (2018). "Squeeze-and-Excitation Networks". 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 7132–7141. arXiv:1709.01507. doi:10.1109/CVPR.2018.00745. ISBN 978-1-5386-6420-9. S2CID 206597034.
- ^ Woo, Sanghyun; Park, Jongchan; Lee, Joon-Young; Kweon, In So (2018-07-18). "CBAM: Convolutional Block Attention Module". arXiv:1807.06521 .
- ^ Georgescu, Mariana-Iuliana; Ionescu, Radu Tudor; Miron, Andreea-Iuliana; Savencu, Olivian; Ristea, Nicolae-Catalin; Verga, Nicolae; Khan, Fahad Shahbaz (2022-10-12). "Multimodal Multi-Head Convolutional Attention with Various Kernel Sizes for Medical Image Super-Resolution". arXiv:2204.04218 .
- ^ Neil Rhodes (2021). CS 152 NN—27: Attention: Keys, Queries, & Values. Event occurs at 06:30. Retrieved 2021-12-22.
- ^ Alfredo Canziani & Yann Lecun (2021). NYU Deep Learning course, Spring 2020. Event occurs at 05:30. Retrieved 2021-12-22.
- ^ Alfredo Canziani & Yann Lecun (2021). NYU Deep Learning course, Spring 2020. Event occurs at 20:15. Retrieved 2021-12-22.
- ^ Robertson, Sean. "NLP From Scratch: Translation With a Sequence To Sequence Network and Attention". pytorch.org. Retrieved 2021-12-22.
- ^ Mittal, Aayush (2024-07-17). "Flash Attention: Revolutionizing Transformer Efficiency". Unite.AI. Retrieved 2024-11-16.
- ^ Lee, Juho; Lee, Yoonho; Kim, Jungtaek; Kosiorek, Adam R; Choi, Seungjin; Teh, Yee Whye (2018). "Set Transformer: A Framework for Attention-based Permutation-Invariant Neural Networks". arXiv:1810.00825 .
External links
- Olah, Chris; Carter, Shan (September 8, 2016). "Attention and Augmented Recurrent Neural Networks". Distill. 1 (9). Distill Working Group. doi:10.23915/distill.00001.
- Dan Jurafsky and James H. Martin (2022) Speech and Language Processing (3rd ed. draft, January 2022), ch. 10.4 Attention and ch. 9.7 Self-Attention Networks: Transformers
- Alex Graves (4 May 2020), Attention and Memory in Deep Learning (video lecture), DeepMind / UCL, via YouTube











































